Sztuczna inteligencja (AI) to systemy komputerowe wykonujące zadania wymagające ludzkiej inteligencji. Działa na podstawie algorytmów matematycznych, głównie sieci neuronowych, które naśladują działanie ludzkiego mózgu. Matematycznie opiera się na macierzach wag połączeń między neuronami, funkcjach aktywacji (np. sigmoid, ReLU) oraz metodach optymalizacji jak gradient descent. AI uczy się minimalizując funkcję straty – różnicę między przewidywaniami a rzeczywistymi wynikami, dostosowując wagi w procesie zwanym backpropagation.
Sieci neuronowe stanowią fundamentalną część aktualnej sztucznej inteligencji, bazując na zaawansowanych koncepcjach matematycznych. Podstawą ich działania jest transformacja danych wejściowych poprzez warstwy neuronów, które wykonują szereg operacji matematycznych. Najważniejszym elementem są funkcje aktywacji, które determinują sposób przetwarzania sygnałów w sieci. Inspirowane biologicznymi mechanizmami mózgu, sieci neuronowe wykorzystują skomplikowane algorytmy do rozpoznawania wzorców i podejmowania decyzji. W procesie uczenia maszynowego szczególnie ważna jest rola gradientów i pochodnych cząstkowych, które umożliwiają optymalizację wag synaptycznych. Matematyczna reprezentacja sieci obejmuje złożone operacje na macierzach i wektorach, gdzie każde dobranie między neuronami ma przypisaną wartość wagową.
Proces uczenia sieci neuronowej opiera się na minimalizacji funkcji straty poprzez algorytm propagacji wstecznej (backpropagation). Jak dokładnie przebieg tego procesu wpływa na końcową efektywność modelu? Optymalizacja parametrów wymaga zrozumienia koncepcji przestrzeni wielowymiarowej i analizy tensorowej. Implementacja sieci neuronowych wykorzystuje zaawansowane biblioteki matematyczne i architekturę wielowarstwową. Zagadnienia takie jak normalizacja wsadowa czy regularyzacja stanowią elementy w zapobieganiu przeuczeniu modelu.
Matematyczne aspekty głębokiego uczenia
- Obliczenia gradientowe w przestrzeniach wielowymiarowych
- Optymalizacja funkcji straty metodami numerycznymi
- Transformacje nieliniowe w warstwach ukrytych
Zaawansowane architektury sieci neuronowych wymagają szczególnego podejścia do optymalizacji: Konwolucyjne sieci neuronowe (CNN) wykorzystują operacje splotu matematycznego do analizy danych przestrzennych, w czasie gdy sieci rekurencyjne (RNN) bazują na sekwencyjnym przetwarzaniu informacji w czasie. Techniki takie jak dropout czy batch normalization wprowadzają element stochastyczny do procesu uczenia. Matematyczne podstawy tych mechanizmów opierają się na teorii prawdopodobieństwa i statystyce.

Optymalizacja i regularyzacja modeli
W praktyce implementacja sieci neuronowych wymaga zbalansowania wielu parametrów: od wyboru odpowiedniej architektury po dostrojenie hiperparametrów. “Głębokie sieci neuronowe potrafią automatycznie wykrywać złożone wzorce w danych, ale wymagają precyzyjnego strojenia”. Zastosowanie technik np. cross-validation czy early stopping pomaga w kontrolowaniu procesu uczenia. Algorytmy optymalizacji: od klasycznego gradientu prostego po zaawansowane metody adaptacyjne (Adam, RMSprop) – stanowią rdzeń procesu treningu.
Fundamenty matematyczne AI: sprawdź tajemnice działania neuronów sztucznych
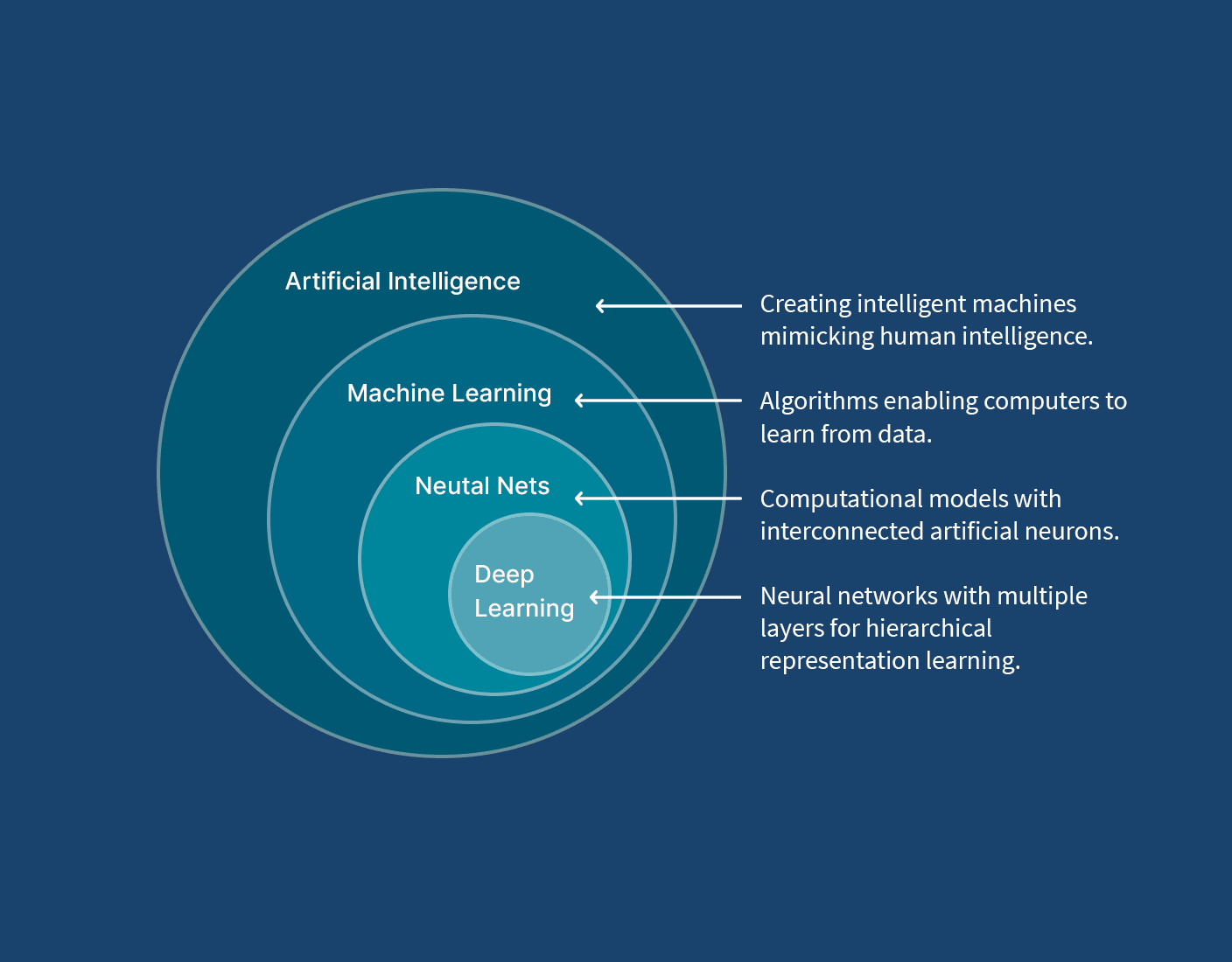
Matematyczne podstawy sieci neuronowych opierają się na złożonych operacjach algebraicznych i funkcjach aktywacji. Najważniejszym elementem jest proces uczenia sieci, który wykorzystuje algorytmy optymalizacji gradientowej do minimalizacji funkcji straty. Każdy neuron w sieci przetwarza dane wejściowe poprzez sumowanie ważone, a następnie aplikuje nieliniową funkcję aktywacji. Ciekawe funkcje aktywacji to ReLU, sigmoid czy tangens hiperboliczny, które wprowadzają do modelu niezbędną nieliniowość.
W procesie treningu sieci neuronowej ogromną rolę odgrywa mechanizm propagacji wstecznej, który pozwala na efektywne obliczanie gradientów i aktualizację wag. Wykorzystuje się tu rachunek różniczkowy i algebrę liniową do optymalizacji parametrów modelu. Architektura głębokich sieci neuronowych wymaga zrozumienia zaawansowanych koncepcji matematycznych, np. przestrzenie wektorowe czy transformacje nieliniowe. Teoria grafów pomaga w analizie połączeń między neuronami, w czasie gdy różnych danycha i teoria prawdopodobieństwa są potrzebne do interpretacji wyników i oceny jakości modelu. Aktualnie implementacje sieci neuronowych korzystają z zaawansowanych bibliotek numerycznych, które optymalizują obliczenia macierzowe i tensorowe.
Rewolucja tensorowa: Jak GPU przekształca świat głębokiego uczenia
Deep learning osiągnął przełomowy rozwój dzięki obliczeniom tensorowym na kartach graficznych. Procesory GPU dają równoległe przetwarzanie danych, to podstawa dla efektywnego trenowania złożonych sieci neuronowych. Architektury takie jak CUDA czy OpenCL umożliwiają wykonywanie tysięcy operacji matematycznych jednocześnie, drastycznie przyspieszając proces uczenia modeli.
- Równoległe przetwarzanie danych
- Optymalizacja pamięci podręcznej
- Dedykowane jednostki tensorowe
- Specjalizowane biblioteki ML
- Skalowanie rozproszone
- Energooszczędność obliczeń
Nowoczesne karty graficzne posiadają dedykowane rdzenie tensorowe, które są zoptymalizowane pod kątem operacji macierzowych wykorzystywanych w sieciach neuronowych. Technologia ta zrewolucjonizowała możliwości obliczeniowe w zakresie sztucznej inteligencji, umożliwiając trenowanie złożonych modeli w rozsądnym czasie.
Kwantowe akceleratory tensorowe: Przyszłość deep learningu
Nowe badania skupiają się na integracji obliczeń kwantowych z procesorami tensorowymi. Hybrydowe rozwiązania łączące klasyczne GPU z elementami kwantowymi mogą potencjalnie przynieść kolejny przełom w wydajności głębokiego uczenia. Eksperymentalne układy już teraz pokazują możliwość przyspieszenia określonych operacji tensorowych nawet stukrotnie w porównaniu do konwencjonalnych GPU.
Potęga języka: Jak transformery i uwaga zmieniły NLP
Transformery to przełomowa architektura sieci neuronowych, która zrewolucjonizowała sposób przetwarzania języka naturalnego. Ich główną innowacją jest mechanizm attention (uwagi), który pozwala modelowi skupić się na ważnych częściach sekwencji wejściowej w czasie przetwarzania danych. W odróżnieniu od tradycyjnych sieci rekurencyjnych (RNN), transformery mogą przetwarzać całe sekwencje równolegle, co przyspiesza proces uczenia i wnioskowania.
Mechanizm attention umożliwia modelowi dynamiczne przypisywanie wag do różnych elementów wejściowych, to podstawa dla zrozumienia kontekstu i relacji między słowami. Transformery wykorzystują wielogłowicową uwagę (multi-head attention), która pozwala na jednoczesne skupienie się na różnych aspektach danych wejściowych. Architektura transformera składa się z warstw kodera i dekodera, które mają moduły self-attention i feed-forward neural networks. Ta konstrukcja umożliwia modelowi wydajne przetwarzanie długich sekwencji tekstowych i jest podstawą wielu nowoczesnych modeli językowych, np. BERT, GPT i T5.
Z pomocą tym innowacjom, transformery osiągają wyjątkowe wyniki w zadaniach NLP, od tłumaczenia maszynowego po generowanie tekstu.